Exclusive Material For IIT-JEE aspirants.
Coming Soon Only On THE EDU ZEAL
Now read the posts of The Edu Zeal by subscribing to our rss feeds or by e-mail

Monday, 14 January 2013

Electricity

The electric field E

Main article: Electric field
The electric field E is defined such that, on a stationary charge:
\mathbf{F} = q_0 \mathbf{E}
where q0 is what is known as a test charge. The size of the charge doesn't really matter, as long as it is small enough not to influence the electric field by its mere presence. What is plain from this definition, though, is that the unit of E is N/C (newtons per coulomb). This unit is equal to V/m (volts per meter), see below.
In electrostatics, where charges are not moving, around a distribution of point charges, the forces determined from Coulomb's law may be summed. The result after dividing by q0 is:
\mathbf{E(r)} = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^{n} \frac{q_i \left( \mathbf{r} - \mathbf{r}_i \right)} {\left| \mathbf{r} - \mathbf{r}_i \right|^3}
where n is the number of charges, qi is the amount of charge associated with the ith charge, ri is the position of the ith charge, r is the position where the electric field is being determined, and ε0 is the electric constant.
If the field is instead produced by a continuous distribution of charge, the summation becomes an integral:
\mathbf{E(r)} = \frac{1}{ 4 \pi \varepsilon_0 } \int \frac{\rho(\mathbf{r'}) \left( \mathbf{r} - \mathbf{r'} \right)} {\left| \mathbf{r} - \mathbf{r'} \right|^3} \mathrm{d^3}\mathbf{r'}
where \rho(\mathbf{r'}) is the charge density and \mathbf{r}-\mathbf{r'} is the vector that points from the volume element \mathrm{d^3}\mathbf{r'} to the point in space where E is being determined.
Both of the above equations are cumbersome, especially if one wants to determine E as a function of position. A scalar function called the electric potential can help. Electric potential, also called voltage (the units for which are the volt), is defined by the line integral
\varphi \mathbf{(r)} = - \int_C \mathbf{E} \cdot \mathrm{d}\mathbf{l}
where φ(r) is the electric potential, and C is the path over which the integral is being taken.
Unfortunately, this definition has a caveat. From Maxwell's equations, it is clear that ∇ × E is not always zero, and hence the scalar potential alone is insufficient to define the electric field exactly. As a result, one must add a correction factor, which is generally done by subtracting the time derivative of the A vector potential described below. Whenever the charges are quasistatic, however, this condition will be essentially met.
From the definition of charge, one can easily show that the electric potential of a point charge as a function of position is:
\varphi \mathbf{(r)} = \frac{1}{4 \pi \varepsilon_0 } \sum_{i=1}^{n} \frac{q_i \left( \mathbf{r} - \mathbf{r}_i \right)} {\left| \mathbf{r} - \mathbf{r}_i \right|}
where q is the point charge's charge, r is the position at which the potential is being determined, and ri is the position of each point charge. The potential for a continuous distribution of charge is:
\varphi \mathbf{(r)} = \frac{1}{4 \pi \varepsilon_0} \int \frac{\rho(\mathbf{r'})}{|\mathbf{r}-\mathbf{r'}|}\, \mathrm{d^3}\mathbf{r'}
where \rho(\mathbf{r'}) is the charge density, and \mathbf{r}-\mathbf{r'} is the distance from the volume element \mathrm{d^3}\mathbf{r'} to point in space where φ is being determined.
The scalar φ will add to other potentials as a scalar. This makes it relatively easy to break complex problems down in to simple parts and add their potentials. Taking the definition of φ backwards, we see that the electric field is just the negative gradient (the del operator) of the potential. Or:
\mathbf{E(r)} = -\nabla \varphi \mathbf{(r)} .
From this formula it is clear that E can be expressed in V/m (volts per meter).

Electromagnetic waves

Main article: Electromagnetic waves
A changing electromagnetic field propagates away from its origin in the form of a wave. These waves travel in vacuum at the speed of light and exist in a wide spectrum of wavelengths. Examples of the dynamic fields of electromagnetic radiation (in order of increasing frequency): radio waves, microwaves, light (infrared, visible light and ultraviolet), x-rays and gamma rays. In the field of particle physics this electromagnetic radiation is the manifestation of the electromagnetic interaction between charged particles.

General field equations

Main articles: Jefimenko's equations and Liénard-Wiechert potentials
As simple and satisfying as Coulomb's equation may be, it is not entirely correct in the context of classical electromagnetism. Problems arise because changes in charge distributions require a non-zero amount of time to be "felt" elsewhere (required by special relativity).
For the fields of general charge distributions, the retarded potentials can be computed and differentiated accordingly to yield Jefimenko's Equations.
Retarded potentials can also be derived for point charges, and the equations are known as the Liénard-Wiechert potentials. The scalar potential is:
\varphi = \frac{1}{4 \pi \varepsilon_0} \frac{q}{\left| \mathbf{r} - \mathbf{r}_q(t_{ret}) \right|-\frac{\mathbf{v}_q(t_{ret})}{c} \cdot (\mathbf{r} - \mathbf{r}_q(t_{ret}))}
where q is the point charge's charge and r is the position. rq and vq are the position and velocity of the charge, respectively, as a function of retarded time. The vector potential is similar:
\mathbf{A} = \frac{\mu_0}{4 \pi} \frac{q\mathbf{v}_q(t_{ret})}{\left| \mathbf{r} - \mathbf{r}_q(t_{ret}) \right|-\frac{\mathbf{v}_q(t_{ret})}{c} \cdot (\mathbf{r} - \mathbf{r}_q(t_{ret}))}.
These can then be differentiated accordingly to obtain the complete field equations for a moving point particle.

Models

A branch of classical electromagnetisms such as optics, electrical and electronic engineering consist of a collection of relevant mathematical models of different degree of simplification and idealization to enhance our understanding of the specific electrodynamics phenomena, cf. An electrodynamics phenomenon is determined by the particular fields, specific densities of electric charges and currents, and the particular transmission medium. Since there are infinitely many of them, in modeling there is a need for some typical, representative
(a) electrical charges and currents, e.g. moving pointlike charges and electric and magnetic dipoles, electric currents in a conductor etc;
(b) electromagnetic fields, e.g. voltages, the Liénard-Wiechert potentials, the monochromatic plane waves , optical rays; radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays , gamma rays etc;
(c) transmission media, e.g. electronic components, antennas, electromagnetic waveguides, flat mirrors, mirrors with curved surfaces convex lenses, concave lenses; resistors, inductors, capacitors, switches; wires, electric and optical cables, transmission lines, integrated circuits etc;
which all have only few variable characteristics.


SOURCE WIKIPEDIA
Posted by at
Labels:

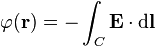
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)