Surface tension is a contractive tendency of the surface of a
liquid
that allows it to resist an external force. It is revealed, for
example, in the floating of some objects on the surface of water, even
though they are denser than water, and in the ability of some insects
(e.g.
water striders) to run on the water surface. This property is caused by
cohesion of similar
molecules, and is responsible for many of the behaviors of liquids.
Surface tension has the
dimension of
force per unit
length, or of
energy per unit
area. The two are equivalent—but when referring to energy per unit of area, people use the term
surface energy—which is a more general term in the sense that it applies also to
solids and not just liquids.
In
materials science, surface tension is used for either
surface stress or
surface free energy.
Causes

Diagram of the forces on molecules of a liquid

Surface tension prevents the paper clip from submerging.
The cohesive forces among liquid molecules are responsible for the
phenomenon of surface tension. In the bulk of the liquid, each molecule
is pulled equally in every direction by neighboring liquid molecules,
resulting in a net force of zero. The molecules at the surface do not
have other molecules on all sides of them and therefore are pulled
inwards. This creates some
internal pressure and forces liquid surfaces to contract to the minimal area.
Surface tension is responsible for the shape of liquid droplets.
Although easily deformed, droplets of water tend to be pulled into a
spherical shape by the cohesive forces of the surface layer. In the
absence of other forces, including
gravity,
drops of virtually all liquids would be perfectly spherical. The
spherical shape minimizes the necessary "wall tension" of the surface
layer according to
Laplace's law.
Another way to view surface tension is in terms of energy. A molecule
in contact with a neighbor is in a lower state of energy than if it
were alone (not in contact with a neighbor). The interior molecules have
as many neighbors as they can possibly have, but the boundary molecules
are missing neighbors (compared to interior molecules) and therefore
have a higher energy. For the liquid to minimize its energy state, the
number of higher energy boundary molecules must be minimized. The
minimized quantity of boundary molecules results in a minimized surface
area.
As a result of surface area minimization, a surface will assume the
smoothest shape it can (mathematical proof that "smooth" shapes minimize
surface area relies on use of the
Euler–Lagrange equation).
Since any curvature in the surface shape results in greater area, a
higher energy will also result. Consequently the surface will push back
against any curvature in much the same way as a ball pushed uphill will
push back to minimize its gravitational potential energy.
Effects of surface tension
Water
Several effects of surface tension can be seen with ordinary water:
A. Beading of rain water on a waxy surface, such as a leaf.
Water adheres weakly to wax and strongly to itself, so water clusters
into drops. Surface tension gives them their near-spherical shape,
because a sphere has the smallest possible surface area to volume ratio.
B. Formation of
drops
occurs when a mass of liquid is stretched. The animation shows water
adhering to the faucet gaining mass until it is stretched to a point
where the surface tension can no longer bind it to the faucet. It then
separates and surface tension forms the drop into a sphere. If a stream
of water were running from the faucet, the stream would break up into
drops during its fall. Gravity stretches the stream, then surface
tension pinches it into spheres.
C. Flotation of objects denser than water occurs when the
object is nonwettable and its weight is small enough to be borne by the
forces arising from surface tension.
For example,
water striders
use surface tension to walk on the surface of a pond. The surface of
the water behaves like an elastic film: the insect's feet cause
indentations in the water's surface, increasing its surface area.
D. Separation of oil and water (in this case, water and liquid
wax) is caused by a tension in the surface between dissimilar liquids.
This type of surface tension is called "interface tension", but its
physics are the same.
E.
Tears of wine
is the formation of drops and rivulets on the side of a glass
containing an alcoholic beverage. Its cause is a complex interaction
between the differing surface tensions of water and
ethanol; it is induced by a combination of surface tension modification of water by
ethanol together with ethanol
evaporating faster than water.
-
A. Water beading on a leaf
-
B. Water dripping from a tap
-
-
D. Lava lamp with interaction between dissimilar liquids; water and liquid wax
-
Surfactants
Surface tension is visible in other common phenomena, especially when
surfactants are used to decrease it:
- Soap bubbles
have very large surface areas with very little mass. Bubbles in pure
water are unstable. The addition of surfactants, however, can have a
stabilizing effect on the bubbles (see Marangoni effect). Notice that surfactants actually reduce the surface tension of water by a factor of three or more.
- Emulsions
are a type of solution in which surface tension plays a role. Tiny
fragments of oil suspended in pure water will spontaneously assemble
themselves into much larger masses. But the presence of a surfactant
provides a decrease in surface tension, which permits stability of
minute droplets of oil in the bulk of water (or vice versa).
Basic physics
Two definitions

Diagram shows, in cross-section, a needle floating on the surface of water. Its weight, F
w, depresses the surface, and is balanced by the surface tension forces on either side, F
s,
which are each parallel to the water's surface at the points where it
contacts the needle. Notice that the horizontal components of the two F
s
arrows point in opposite directions, so they cancel each other, but the
vertical components point in the same direction and therefore add up
to balance F
w.
Surface tension, represented by the symbol
γ
is defined as the force along a line of unit length, where the force is
parallel to the surface but perpendicular to the line. One way to
picture this is to imagine a flat soap film bounded on one side by a
taut thread of length,
L. The thread will be pulled toward the interior of the film by a force equal to 2
 L
L (the factor of 2 is because the soap film has two sides, hence two surfaces).
Surface tension is therefore measured in
forces per
unit length. Its
SI unit is
newton per meter but the
cgs unit of
dyne per cm is also used.
One dyn/cm corresponds to 0.001 N/m.
An equivalent definition, one that is useful in
thermodynamics, is
work done per unit area. As such, in order to increase the surface area of a mass of liquid by an amount,
δA, a quantity of work,
 δA
δA, is needed.
This work is stored as potential energy. Consequently surface tension
can be also measured in SI system as joules per square meter and in the
cgs system as
ergs per cm
2.
Since mechanical systems try to find a state of minimum potential
energy, a free droplet of liquid naturally assumes a spherical shape,
which has the minimum surface area for a given volume.
The equivalence of measurement of energy per unit area to force per unit length can be proven by
dimensional analysis.
Surface curvature and pressure

Surface tension forces acting on a tiny (differential) patch of surface.
δθx and
δθy indicate the amount of bend over the dimensions of the patch. Balancing the tension forces with pressure leads to the
Young–Laplace equation
If no force acts normal to a tensioned surface, the surface must
remain flat. But if the pressure on one side of the surface differs from
pressure on the other side, the pressure difference times surface area
results in a normal force. In order for the surface tension forces to
cancel the force due to pressure, the surface must be curved. The
diagram shows how surface curvature of a tiny patch of surface leads to a
net component of surface tension forces acting normal to the center of
the patch. When all the forces are balanced, the resulting equation is
known as the
Young–Laplace equation:
-
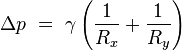
where:
-
- Δp is the pressure difference.
 is surface tension.
is surface tension.- Rx and Ry are radii of curvature in each of the axes that are parallel to the surface.
The quantity in parentheses on the right hand side is in fact (twice) the
mean curvature of the surface (depending on normalisation).
Solutions to this equation determine the shape of water drops,
puddles, menisci, soap bubbles, and all other shapes determined by
surface tension (such as the shape of the impressions that a water
strider's feet make on the surface of a pond).
The table below shows how the internal pressure of a water droplet
increases with decreasing radius. For not very small drops the effect is
subtle, but the pressure difference becomes enormous when the drop
sizes approach the molecular size. (In the limit of a single molecule
the concept becomes meaningless.)
| Δp for water drops of different radii at STP |
| Droplet radius |
1 mm |
0.1 mm |
1 μm |
10 nm |
| Δp (atm) |
0.0014 |
0.0144 |
1.436 |
143.6 |
Liquid surface
To find the shape of the
minimal surface
bounded by some arbitrary shaped frame using strictly mathematical
means can be a daunting task. Yet by fashioning the frame out of wire
and dipping it in soap-solution, a locally minimal surface will appear
in the resulting soap-film within seconds
The reason for this is that the pressure difference across a fluid interface is proportional to the
mean curvature, as seen in the
Young-Laplace equation.
For an open soap film, the pressure difference is zero, hence the mean
curvature is zero, and minimal surfaces have the property of zero mean
curvature.
Contact angles
Main article:
Contact angle
The surface of any liquid is an interface between that liquid and some other medium
The top surface of a pond, for example, is an interface between the
pond water and the air. Surface tension, then, is not a property of the
liquid alone, but a property of the liquid's interface with another
medium. If a liquid is in a container, then besides the liquid/air
interface at its top surface, there is also an interface between the
liquid and the walls of the container. The surface tension between the
liquid and air is usually different (greater than) its surface tension
with the walls of a container. And where the two surfaces meet, their
geometry must be such that all forces balance.
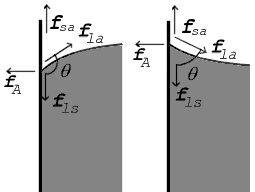
Forces at contact point shown for contact angle greater than 90° (left) and less than 90° (right)
|
Where the two surfaces meet, they form a
contact angle,

,
which is the angle the tangent to the surface makes with the solid
surface. The diagram to the right shows two examples. Tension forces are
shown for the liquid-air interface, the liquid-solid interface, and the
solid-air interface. The example on the left is where the difference
between the liquid-solid and solid-air surface tension,
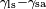
, is less than the liquid-air surface tension,

, but is nevertheless positive, that is
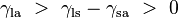
In the diagram, both the vertical and horizontal forces must cancel exactly at the contact point, known as
equilibrium. The horizontal component of
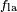
is canceled by the adhesive force,
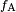
.
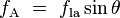
The more telling balance of forces, though, is in the vertical direction. The vertical component of
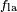
must exactly cancel the force,

.
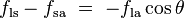
Since the forces are in direct proportion to their respective surface tensions, we also have
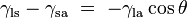
where
-
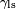 is the liquid-solid surface tension,
is the liquid-solid surface tension,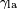 is the liquid-air surface tension,
is the liquid-air surface tension, is the solid-air surface tension,
is the solid-air surface tension, is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.
is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.
This means that although the difference between the liquid-solid and solid-air surface tension,

, is difficult to measure directly, it can be inferred from the liquid-air surface tension,
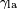
, and the equilibrium contact angle,

, which is a function of the easily measurable advancing and receding contact angles (see main article contact angle).
This same relationship exists in the diagram on the right. But in
this case we see that because the contact angle is less than 90°, the
liquid-solid/solid-air surface tension difference must be negative:

Special contact angles
Observe that in the special case of a water-silver interface where
the contact angle is equal to 90°, the liquid-solid/solid-air surface
tension difference is exactly zero.
Another special case is where the contact angle is exactly 180°. Water with specially prepared
Teflon approaches this. Contact angle of 180° occurs when the liquid-solid surface tension is exactly equal to the liquid-air surface tension.




 , where g is the acceleration due to gravity (9.8 N/kg). This last expression comes from equating the kinetic energy gained,
, where g is the acceleration due to gravity (9.8 N/kg). This last expression comes from equating the kinetic energy gained,  , with the potential energy lost, mgh , and solving for v.
, with the potential energy lost, mgh , and solving for v. ) is the energy released as heat when a compound undergoes complete combustion with oxygen under standard conditions. The chemical reaction is typically a hydrocarbon reacting with oxygen to form carbon dioxide, water and heat. It may be expressed with the quantities:
) is the energy released as heat when a compound undergoes complete combustion with oxygen under standard conditions. The chemical reaction is typically a hydrocarbon reacting with oxygen to form carbon dioxide, water and heat. It may be expressed with the quantities: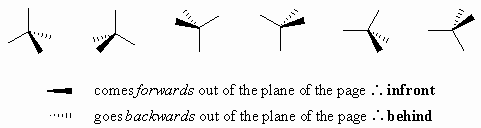
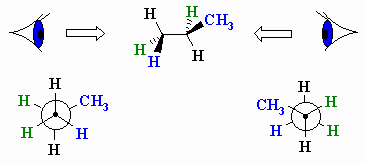
 Sawhorse diagrams are similar to wedge-dash diagrams, but without
trying to use "shading" to denote the perspective. The representation to the
right of propane has been drawn so that we are looking at the molecule which
is below us and to our left.
Sawhorse diagrams are similar to wedge-dash diagrams, but without
trying to use "shading" to denote the perspective. The representation to the
right of propane has been drawn so that we are looking at the molecule which
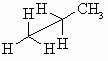
is below us and to our left. 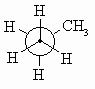 These
projections are drawn by looking directly along a particular bond in the system
(here a C-C bond) and arranging the substituents symmetrically around the atoms
at each end of that bond. The protocol requires that the atoms within the central
bond are defined as shown below:
These
projections are drawn by looking directly along a particular bond in the system
(here a C-C bond) and arranging the substituents symmetrically around the atoms
at each end of that bond. The protocol requires that the atoms within the central
bond are defined as shown below: 











 L (the factor of 2 is because the soap film has two sides, hence two surfaces).
L (the factor of 2 is because the soap film has two sides, hence two surfaces).
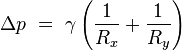


 ,
which is the angle the tangent to the surface makes with the solid
surface. The diagram to the right shows two examples. Tension forces are
shown for the liquid-air interface, the liquid-solid interface, and the
solid-air interface. The example on the left is where the difference
between the liquid-solid and solid-air surface tension,
,
which is the angle the tangent to the surface makes with the solid
surface. The diagram to the right shows two examples. Tension forces are
shown for the liquid-air interface, the liquid-solid interface, and the
solid-air interface. The example on the left is where the difference
between the liquid-solid and solid-air surface tension, 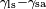 , is less than the liquid-air surface tension,
, is less than the liquid-air surface tension,  , but is nevertheless positive, that is
, but is nevertheless positive, that is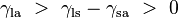
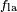 is canceled by the adhesive force,
is canceled by the adhesive force, 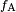 .
.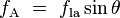
 .
.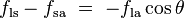
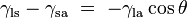
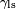 is the liquid-solid surface tension,
is the liquid-solid surface tension,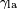 is the liquid-air surface tension,
is the liquid-air surface tension, is the solid-air surface tension,
is the solid-air surface tension, , is difficult to measure directly, it can be inferred from the liquid-air surface tension,
, is difficult to measure directly, it can be inferred from the liquid-air surface tension, 
